GSL 简介

gsl（GNU Scientific Library）是专门为应用数学和科学技术领域的数值计算提供支持的软件库。gsl使用C语言编写，同时也为其他语言做了相应的封装。gsl在GNU通用公共许可下是免费的。该函数库提供了广泛的数学算法的实现函数，包括随机数生成器，特殊函数和最小二乘拟合等等。目前该函数库提供有超过1000个函数，这些函数包含的范围有：复数计算、多项式求根、特殊函数、向量和矩阵运算、排列、组合、排序、线性代数、特征值和特征向量、快速傅里叶变换(FFT)、数值积分、随机数生成、随机数分布、统计、蒙特卡洛积分、模拟退火、常微分方程组、插值、数值微分、方程求根、最小二乘拟合、小波变换等

GSL 下载

下载GSL安装文件： 链接: http://mirrors.ustc.edu.cn/gnu/gsl.

GSL文档在线：链接:https://www.gnu.org/software/gsl/doc/html/index.html.

GSL文档下载：链接:https://www.gnu.org/software/gsl/doc/latex/gsl-ref.pdf.

GSL安装

1. 解压压缩包：$ tar -zxvf gsl-2.7.tar.gz
Alt
2. 创建安装目录:$ mkdir /home/ccchenji/Desktop/gsl_gcc

注意：ccchenji是我系统的用户名，这里要换成你的系统的用户名。

3. 进入源码目录:$ cd /home/ccchenji/Desktop/gsl-2.7

注意：ccchenji是我系统的用户名，这里要换成你的系统的用户名。

4.配置configure文件

1
2
3
4
5
6
7
8
9
# 参数含义
# CC:指定编译工具链
# --prefix: 指定库的安装目录
# --host: 指定安装平台,可选，交叉编译要制定安装平台如在arm上编译 --host=arm
# ./configure -h: 可以得到配置的帮助信息

# linux上安装
$ ./configure CC="gcc" --prefix=/home/ccchenji/Desktop/gsl_gcc
#注意：ccchenji是我系统的用户名，这里要换成你的系统的用户名。

5.使用make进行编译

1
$ make

6.使用make install进行安装

1
$ make install

7.使用make installcheck检查安装是否成功

1
$ make installcheck

GSL使用

1.新建工程文件夹

1
2
$ mkdir /home/ccchenji/Desktop/gsl_test
#注意：ccchenji是我系统的用户名，这里要换成你的系统的用户名。

2.新建makefile文件并编辑

1
2
3
4
#进入gsl_gcc文件夹并新建makefile文件
$ touch makefile
# 编辑makefile文件
$ vim makefile

makefile文件内容（如果出现错误注意tab的缩进，gcc前要求一个tab的缩进，最好自己手敲一遍，直接粘贴可能出问题）

1
2
3
4
5
6
7
8
9
10
#注意：ccchenji是我系统的用户名，这里要换成你的系统的用户名。
IPATH=-I/home/ccchenji/Desktop/gsl_gcc/include
LPATH=-L/home/ccchenji/Desktop/gsl_gcc/lib
#这里直接链接的静态库文件
main:main.c
	gcc main.c $(IPATH)  $(LPATH) -l:libgsl.a -l:libgslcblas.a -o main

.PHONY:clean
clean:
	rm -rf main

3.新建main.c文件并编辑

1
2
3
4
#进入gsl_gcc文件夹并新建main.c文件
$ touch main.c
# 编辑makefile文件
$ vim main.c

main.c文件内容

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include <stdio.h>
#include <gsl/gsl_matrix.h>
int main (void)
{
        int i, j;
        gsl_matrix * m = gsl_matrix_alloc (10, 3);
        for (i = 0; i < 10; i++)
                for (j = 0; j < 3; j++)
                        gsl_matrix_set (m, i, j, 0.23 + 100*i + j);
        for (i = 0; i < 100; i++)
                for (j = 0; j < 3; j++)
                        printf ("m(%d,%d) = %g\n", i, j,
                                        gsl_matrix_get (m, i, j));
        gsl_matrix_free (m);
        return 0;
}

4.使用make命令编译main.c文件

1
2
3
4
$ make
#编译后生成main文件
#运行main文件
$ ./main

运行结果
Alt

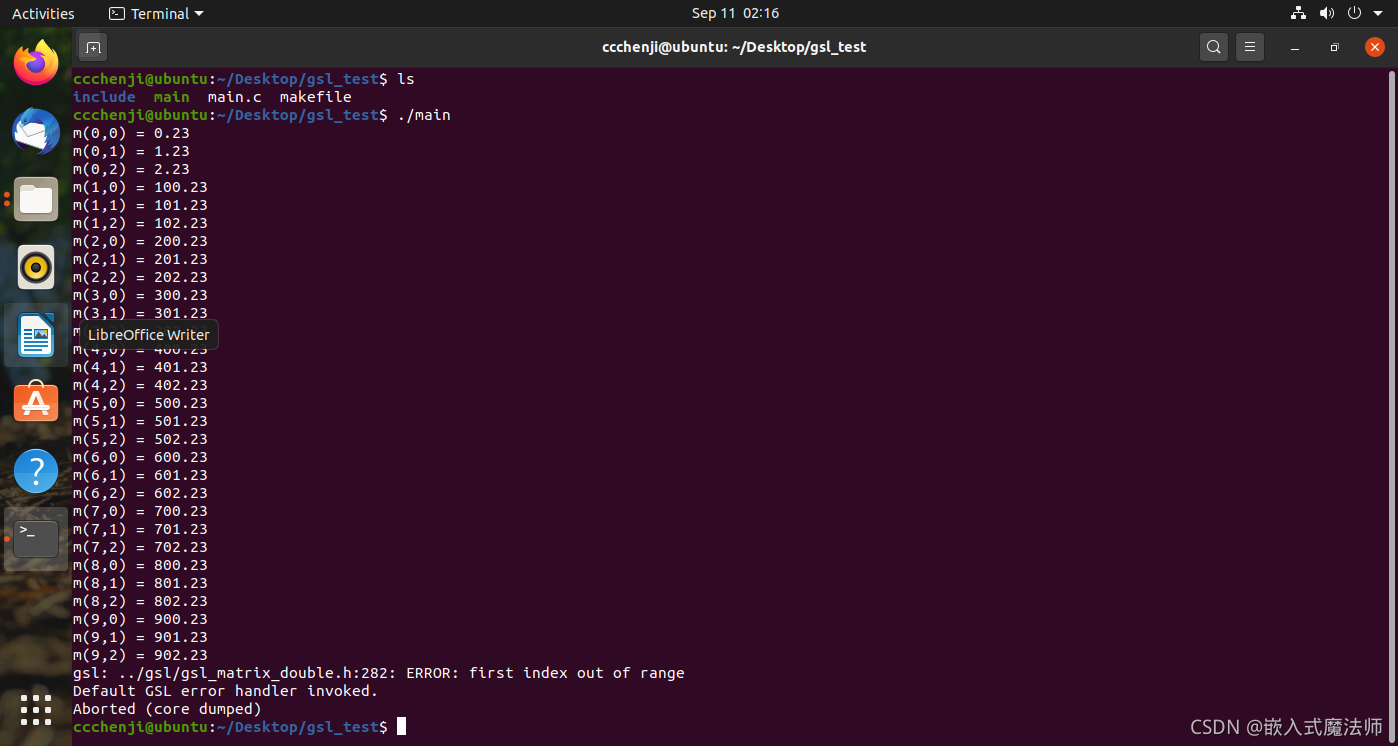
GSL常用函数（持续更新）

矩阵运算

1.Matrix operations 详见手册8.4.9

1
2
3
4
5
6
7
8
9
10
11
12
13
/*
	This function adds the elements of matrix b to the elements of matrix a. 
 	The result a(i, j) ← a(i, j) + b(i, j) is stored in a and b remains unchanged. 
 	The two matrices must have the same dimensions.
*/
int gsl_matrix_add(gsl_matrix *a, const gsl_matrix *b)
/*
This function subtracts the elements of matrix b from the elements of matrix a. 
The result a(i, j) ← a(i, j) − b(i, j) is stored in a and b remains unchanged. 
The two matrices must have the same dimensions.
*/
int gsl_matrix_sub(gsl_matrix *a, const gsl_matrix *b)

2.矩阵乘法

要使用用gcc编译gsl_blas_dgemm 函数必须使用动态库，静态库链接会报错(交叉编译工具链默认使用静态库，对交叉编译工具链，可以使用静态库)

1.配置动态链接库路径

1
2
3
4
#编辑.bashrc文件
$ vim /home/ccchenji/.bashrc
#在文件末尾加入以下代码，以下代码的作用是将动态连接库加入到gcc默认搜索路径
export LD_LIBRARY_PATH=/home/ccchenji/Desktop/gsl_gcc/lib:$LD_LIBRARY_PATH

2.重写makefile文件

1
2
3
4
5
6
7
8
9
IPATH=-I/home/ccchenji/Desktop/gsl_gcc/include
LPATH=-L/home/ccchenji/Desktop/gsl_gcc/lib
#gcc 这里链接动态库
main:main.c
        gcc main.c $(IPATH)  $(LPATH) -lm -lgsl -lgslcblas -o main

.PHONY:clean
clean:
        rm -rf main

3.gsl_blas_dgemm()函数说明

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
//函数原型
int gsl_blas_dgemm( CBLAS_TRANSPOSE_t TransA, 
					CBLAS_TRANSPOSE_t TransB, 
					double alpha,
					const gsl_matrix *A,
					const gsl_matrix *B, 
					double beta, 
					gsl_matrix *C)
/*
参数说明
1.CBLAS_TRANSPOSE_t 可取值: 
  CblasNoTrans：矩阵不需要转置
  CblasTrans: 矩阵需要转置
2.alpha、beta数乘系数
3.计算表达式： C = alpha * op( A ) * op( B ) + beta * C
*/

4.gsl_blas_dgemm()函数使用例程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
include <stdio.h>
#include <gsl/gsl_blas.h>
#include <math.h>
int main (void)
{
        double a[] = { 0.11, 0.12, 0.13,
                0.21, 0.22, 0.23 };
        double b[] = { 1011, 1012,
                1021, 1022,
                1031, 1032 };
        double c[] = { 0.00, 0.00,
                0.00, 0.00 };
        gsl_matrix_view A = gsl_matrix_view_array(a, 2, 3);
        gsl_matrix_view B = gsl_matrix_view_array(b, 3, 2);
        gsl_matrix_view C = gsl_matrix_view_array(c, 2, 2);
        /* Compute C = A B */
        gsl_blas_dgemm (CblasNoTrans, CblasNoTrans,
                        1.0, &A.matrix, &B.matrix,
                        0.0, &C.matrix);
        printf ("[ %g, %g\n", c[0], c[1]);
        printf (" %g, %g ]\n", c[2], c[3]);
        return 0;
}

2.矩阵求逆

示例代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <stdio.h>
#include <gsl/gsl_linalg.h>

int main (void)
{
        double a_data[] = { 1.0, 0.6, 0.0,
                0.0, 1.5, 1.0,
                0.0, 1.0, 1.0 };
        /*
         * Inverse is
         *    1  -1.2   1.2
         *    0   2.0  -2.0
         *    0  -2.0   3.0
         */
        double inva[9];
        int s, i, j;

        gsl_matrix_view m
                = gsl_matrix_view_array(a_data, 3, 3);
        gsl_matrix_view inv
                = gsl_matrix_view_array(inva,3,3);
        gsl_permutation * p = gsl_permutation_alloc (3);

        printf("The matrix is\n");
        for (i = 0; i < 3; ++i)
                for (j = 0; j < 3; ++j)
                        printf(j==2?"%6.3f\n":"%6.3f ", gsl_matrix_get(&m.matrix,i,j));

        gsl_linalg_LU_decomp (&m.matrix, p, &s);    
        gsl_linalg_LU_invert (&m.matrix, p, &inv.matrix);

        printf("The inverse is\n");
        for (i = 0; i < 3; ++i)
                for (j = 0; j < 3; ++j)
                        printf(j==2?"%6.3f\n":"%6.3f ",gsl_matrix_get(&inv.matrix,i,j));
        gsl_permutation_free (p);
        return 0;
}